Introduction to Crystal Structure

I talked a lot about mechanics in my previous posts, but there is another field that is critically important to understanding material behavior. That field is called materials science, and it focuses on the study of the various properties of materials. It's a fascinating field, covering atomic-level structure and bonding to macroscopic behavior such as stress-strain relations and the origins of plasticity. In many ways, the rather general field of materials science owes its origins to the much older field of metallurgy (the study of metals specifically).

So let's talk some mat sci (or materials science, if you're not into brevity… man.), specifically: crystal structure and defects in crystalline materials. As an aside, I'm kind of an odd duck for a mechanical engineer when it comes to this stuff: nanoscale mechanics was my bread and butter for almost a decade. I find this stuff as fascinating as continuum mechanics.

Crystal Structure

In my previous posts, I assumed our materials were continuous. This, of course, is not strictly accurate. There are a number of features at small length-scales that are discrete, but their combined effect can be smoothed out over long length-scales via material constitutive relations. So what's the real deal?

Metals such as Iron, Aluminum (and their alloys) in solid form are classic examples of a crystalline material. In other words, they have a definite repeating structure at the atomic scale. Liquids and gasses are noncrystalline by definition. But not all solid materials are crystalline: materials such as polymers and many organic compounds are typically amorphous (lacking long range order). Ordinary silicate window glass, for example, is a commonly known amorphous solid. Strictly speaking, there is also another category: quasi-crystals, which exhibit a definite local structure, but not repetitive order (they lack periodicity).

At a length scale on the order of 1-10 nm (\(1-10\mathrm{x}10^{-9}\)m), we find materials have a unit cell, a periodically repeating unit of a group of atoms that make up a crystalline material. There are 14 basic categories, called Bravais lattices:

Bravais lattices. Image from http://www.seas.upenn.edu/~chem101/sschem/solidstatechem.html

The above lattices are based on a single atom basis. A basis is the minimum number of repeating atom units within the unit cell. For example, gold (Au) is an face-centered cubic (FCC) metal that has only one atom in its basis. Meanwhile, diamond, a form of carbon (C), has an FCC lattice but a two atom basis (2 C atoms). In other words, it has a unit of 2 atoms that are placed at each point in an FCC lattice. This produces the diamond cubic structure:

Diamond cubic structure of diamond. The black spheres denote the first carbon atom in the basis, and the light grey spheres denote the second. Size is used to help differentiate the atoms in the basis, and is totally not because I recycled an image of another material.

For a given lattice, there are several parameters that can be used to define the size and shape of a specific unit cell. These lattice parameters are the lengths of each side of the unit cell, and the angles between them. For example, the lattice parameter for gold is 4.08 Å (\(4.08\mathrm{x}10^{-10}\) m). The angles are generally excluded for cubic, tetragonal and orthorhombic systems because they are all 90 degrees when the cell is undeformed.

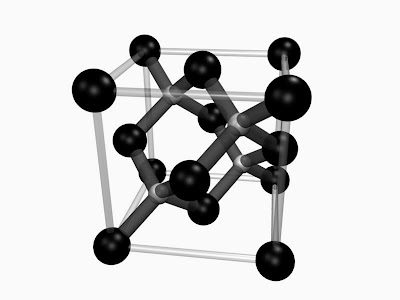
The particular structure a material will take depends on the details of the interatomic interactions. In other words: the bonding between the atoms. A change in crystal structure will generally affect the properties of the material. To use a common example: for carbon, three stable forms exist: diamond, graphite, and amorphous carbon ('carbon black'):

A) Diamond (diamond cubic). B) Graphite (hexagonal). Image courtesy of wikimedia commons. C) Amorphous carbon (amorphous). Image courtesy of Mstroek via wikimedia commons.

Each of these forms (sometimes called allotropes, polymorphs, or phases) requires specific conditions to form from elemental carbon, but the resulting structures are relatively stable across a wide range of temperatures and pressures. They also have radically varied mechanical, thermal and electrical properties: diamond is much harder than graphite, for example.

If we look at iron (Fe), there are several stable polymorphs, depending on the temperature (assuming atmospheric pressure):

• \(\alpha\)-Fe or ferrite, BCC (<910 C)
• \(\gamma\)-Fe or austenite, FCC (910 - 1394 C)
• \(\delta\)-Fe, BCC (1394 - 1538 C)

And above 1538 C, there is a transition to the liquid phase of iron (i.e. it melts).

To give you an idea of what some other materials' unit cells look like, I've included some images of materials I've worked on in the past. The first is the cubic phase of silicon carbide (3C-SiC, a hard ceramic) and the second is a hydrogen storage material known by its chemical formula as \(\mathrm{Li}_4\mathrm{BN}_3\mathrm{H}_{10}\):

A) Structure of 3C-SiC. Red spheres denote Si, blue C. Diamond cubic structure with a lattice parameter of about 4.36 Ang. B) The unit cell of Li4BN3H10. Green spheres are Li, pink are N, brown are B and white are H. Cubic unit cell (BCC symmetry with a large basis) with a lattice parameter of about 10.6 A.

An interesting aspect about atomic structure is the concept of a metastable phase. In other words, a crystal structure that can be made stable only under certain conditions. We'll talk a bit more about that when we get to discussing steel in a later post.

Wait… where does this all come from?

How do we actually learn about the crystal structure of a given material? The most common experimental approach is through diffraction, typically X-ray diffraction or XRD. In essence, what XRD does is bounce x-rays off a sample and measures the pattern produced by the x-rays as they are diffracted by the material. We are able to correlate the angles at which the diffracted x-rays are found to the distances between atoms, specific planes of atoms and even determine things such as lattice parameters or atomic positions within the unit cell. The detailed study of crystal structures is called crystallography, and plays an important role in materials science. There are theoretical approaches as well, based on using models of interatomic bonding with varying levels of detail, to predict possible crystal structures that can then be refined and verified experimentally.

Crystal Orientation and Material Properties

The atomic structure of a material has many important ramifications: the macroscopic properties often of interest in a traditional engineering context are the result of behavior at much smaller length scales. For example, the temperature we measure at the surface of a chunk of steel is actually a measure of the vibrations of the atoms in the unit cell. The expansion (or contraction, in some rare cases) of a solid as it warms up and eventually becomes a liquid is a consequence of the bonding between the atoms. So too is the stiffness we measure at the macroscopic level as the Young's Modulus.

The crystal structure itself has another important aspect: material properties are not generally the same in every direction in a crystal. This relates to the symmetry of the crystal structure, so equivalent directions will have the same properties. For example, if I stretched an FCC lattice perpendicular to one of the faces, I'd expect the same stiffness regardless of the face I chose to move. But if I pulled on a corner instead, I'd expect a different value than I'd found for the face because they are not equivalent. This is called anisotropy. If all of the directions had the same response, then the system would be isotropic. Let's take the case of the Young's Modulus in \(\alpha\)-iron:

• [100] : 125.0 GPa
• [110] : 210.5 GPa
• [111]: 272.7 GPa

Where the bracketed terms denote specific crystallographic directions. Graphically, here is what these directions represent in a cubic system (like \(\alpha\)-iron):

Schematic of crystallographic directions.

Or to put it another way, the numbers are a vector in the basis of the lattice unit vectors.  For specific planes, the convention is to denote them by the plane's normal vector, but in parentheses. For example, (100) would be the positive x-face of a cubic crystal:

Sechematic of crystallographic planes, image from wikimedia commons.

The components of the vector (i.e. [hkl]) are called Miller indices.  There are 3 of them (h,k,l) for all but hexagonal and rhombohedral systems, which instead use a four-index system that we won't get into here.  There's another convention for families of equivalent directions: they are denoted as <hkl>, while families of equivalent planes are denoted as {hkl}.

Defects in Single Crystals

Real materials are not entirely perfect crystals, they have defects, or flaws. These defects play a big role in determining the properties of a material. They can be broken down into several types:

• Point defects
• Line defects
• Interfacial defects
• Bulk defects

Point Defects

Point defects include vacancies or missing atoms in a lattice, interstitials or atoms inserted between lattice sites, and substitutional defects or atom of type B replacing an atom of type A in a lattice. Defects have a formation energy, the energy required to create a single defect in an otherwise perfect (and infinite) lattice from a thermodynamic stand point. What this means is that the formation energy is a measure of the difference in energy between two equilibrium configurations. One interesting ramification of a finite formation energy is that at temperatures above absolute zero, we should expect to find some non-zero concentration of point defects, and that concentration will increase with temperature (more energy available to create defects).

Simple schematic of transition from a low energy state to a stable higher energy state, such as a defect.

The formation energy does not account for the kinetics of defect formation (the actual process and rate of creating the defect). In reality there are intermediate unstable stages with larger changes in energy than the formation energy (see image above). The largest energy difference is called the energy barrier for the formation of the defect. In some cases, the energy barrier is so large that the rate at which defects get formed is very low. In fact, it is entirely possible for the timescale to be so large that for any reasonable amount of time, the system never generates a defect. In such cases, the system is referred to as kinetically stable and is an example of a metastable system. This concept of kinetic versus thermodynamic stability applies to any change in structure, something we'll explore more in a later post as it plays a role in heat treatment of metals.

To give some examples of how point defects are important: they play a role in alloying as we'll discuss this later in this post. They also play a role in hydrogen embrittlement, an undesirable process during arc welding that can lead to weld failure. Another place point defects are important is radiation damage of the cladding of nuclear reactors, where high energy neutrons or fission fragments collide with the walls of the reactor and create chains of point defects called displacement cascades. These point defects can eventually lead to mechanical failure of the cladding.

Line Defects

Line defects, or dislocations, can be broken down into two types: edge dislocations and screw dislocations. A line defect with characteristics of both is called a mixed dislocation.

Edge dislocations can be thought of as an extra partial plane of atoms inserted into a crystal structure:

Schematic of an edge dislocation. The inverted 'T' indicates the dislocation line, which can be thought of as where the 'extra' plane of atoms starts.

The result of the plane's insertion is that the surrounding structure distorts to accommodate it, resulting in a higher energy structure. This localized deformation compared to the ideal lattice also corresponds to internal stresses at the continuum level. If you were to apply a sufficient shear stress to the structure with the edge dislocation you'd end up getting something like the following:

Schematic of edge dislocation migration due to applied shear force.

Note that the dislocation moves due to the change in the position of the top half of the atoms relative to the bottom half. Because the motion of the atoms results in thermodynamically stable states as the dislocation moves, the structural changes do not reverse when the shear stress is removed. To put it in continuum mechanics terms: we've plastically deformed our material because we moved the dislocation. This mechanism of plastic deformation by motion of dislocations is called slip.

Screw dislocations are harder to put into words, so I'll just use a picture:

Schematic of a screw dislocation. The line A-D-C shows the boundary of one side of the dislocation. Image from here.

The concept of dislocation motion still applies to screw dislocations, but the mechanism of motion is a bit different. Screw dislocations actually move perpendicular to the applied shear, while edge dislocations move parallel to it. So an applied shear on the top and bottom surfaces in the above diagram would result in an 'unzipping' of the plane in which the dislocation lies.

A note about the slip planes: the force (and energy) necessary to move a dislocation in a given plane is not the same for all planes. As it ends up, the shear (and energy) necessary to move a dislocation increases with the distance between atomic planes in the direction of the motion of the dislocation. The so-called 'close-packed' planes, planes where the number of atoms per distance is highest, have the smallest distance between atoms and the lowest resistance to slip. These close-packed planes are thus called the slip planes for the given crystal. Because of the number of equivalent close-packed planes in BCC and FCC structures, materials with these structures tend to exhibit high ductility (this includes a number of metals).

Finally, within the slip planes there is a preferred direction of dislocation motion. This preferred direction is creatively called the slip direction. The combination of a slip plane and a slip direction in a crystal is called a slip system for that crystal. As an example, FCC structures exhibit 12 slip systems: four unique slip planes ({111}) with three slip directions (\(<1\bar{1}0>\)) in each plane.

Interfacial and Bulk Defects

I'll just touch briefly on these two categories of defects here.

Interfacial defects are boundaries between distinct regions in a crystal. One example is an external surface, which can be thought of as an interface between the crystal and air, vacuum or something else that doesn't form a bond. Near surfaces the crystal structure tends to relax into a different configuration and may even reorganize, resulting in a reduction in energy compared to the unrelaxed structure.  Another example of interfacial defects are grain boundaries, which will be covered in a later section.

Bulk defects are defects which are present at larger length scales. These include pores, voids, inclusions (a particle of some non-native phase), and cracks. These types of defects are usually created during fabrication and material processing, and processes are generally controlled to minimize their ill effects (sometimes they can be beneficial, depending on the application).

Solid Solutions and Alloys

If we were to add some relatively small number of individual atoms of type B in to a lattice of type A, we'd be creating a number of interstitial defects as discussed earlier. But if the fraction of type B is small compared to A, and the B atoms were well dispersed, we'd expect little change in the overall structure of the material. Even if some of the defects were substitutional, we'd expect little change over a reasonably large lengthscale. This combination of atoms of A and B would then be known as a solid solution, where A is the solvent and B is the solute.

There are several important features that determine the extent to which a group of atoms will form a solid solution:

• Size: atomic radii of the solute atoms need to be similar to the solvent atoms (~15% difference or less)
• Crystal structure: the base crystal structure of the solute and solvent must be similar for high solubility.
• Electronegativity: the electronegativity (tendency to gain or lose electrons in a bond) must be similar.
• Valence:  the number of valence (outer shell) electrons must be similar

An alloy is typically defined as a solid solution where the solvent is a metal. Steels (iron-carbon solid solution, usually with other stuff as well) are probably the best known examples of an alloy used in an engineering context. From a more historical context, bronze is a man-made solid solution of copper and tin that had a dramatic effect on civilization.

One important ramification of the idea of a solid solution is the idea of precipitation. Similar to precipitation of a solid solute from a liquid solution, this occurs when the solvent does not have the ability to accept or maintain some portion of the solute, resulting in the formation of a solid phase made of only the solute. This new phase is called a precipitate. In alloys, the controlled creation of precipitates can create defects that impede the motion of dislocations, leading to a hardening effect. This effect is called precipitation hardening.

Polycrystalline Materials and Grain Boundaries

Not all materials occur in single crystals, where the entire material exists in a single unbroken and unchanging periodic structure. Many metals of engineering interest, such as steels, are much more commonly found in a polycrystalline state. Polycrystalline simply means that the structure is made up of different crystals of varying size and orientation. This may be different unit cells, or just different orientations of the same unit cell grouped in various ways. The individual sections of a polycrystalline material which are of the same type are called grains. The boundaries where these grains meet are called grain boundaries, and play a major role in plastic deformation. If you've ever seen a sheet of galvanized sheet steel, the pattern you may have noticed on the surface is actually the zinc grains that form during the galvanization process. It's worth noting also that the grain size you see in common galvanized coatings can be much larger than the grain size of the underlying metal.

Example of grains and grain boundaries: a simple sheet of galvanized sheet steel. Image courtesy of wikimedia commons.

Polycrystallinity has some interesting ramifications. Recall that material properties can vary based on orientation of the crystal. In a polycrystalline material, the grains are typically going to be arranged somewhat randomly (this is not strictly true, as it is possible to control grain growth to some extent, but it holds for common materials). This means that if you take a macroscopic sample of a metal with a reasonably small grain size, you will have many, many different crystal orientations in the sample. The net effect being that the variations of properties tend to smear themselves out, creating more isotropy than you'd expect at the individual grain level. This is why we can use material models that assume a certain level of isotropy without losing too much accuracy.

The grain boundaries themselves also present some interesting aspects. Firstly, they tend to be a place where certain types of defects, such as dislocations, have trouble propagating. The slip between planes of atoms in a crystal is the main mechanism for plastic deformation in a crystalline material, as discussed earlier. Therefore, impeding their motion leads to a strengthening (increase in yield stress) of the material. By reducing the size of individual grains, you increase the number of grain boundaries in a given sample size, and therefore increase the disruption of dislocation motion. This is called the Hall-Petch Effect, and its effect on the yield stress can be described in terms of material specific constants \(\sigma_0 and k\) and the average grain size (d):
\[\sigma_y = \sigma_0 + k d^{-1/2}\]
Note that as you decrease grain size, the amount of strength gained decreases as the grain size decreases, so there are diminishing returns to contend with.

We'll revisit this topic in a post discussing phase diagrams and heat treatment.

Atomic Structure, Newtonian Mechanics and Quantum Mechanics

Note that in the images that I've been using, I'm representing the atoms as solid spheres: this is a common convention for visual representations. The reality is a bit messier, however, even without getting into the physics of subnuclear particles. It's much better to think of the lattice as made of reference points, and the actual crystal structure will on average resemble it. Why is this?

At a basic level, an atom consists of a group of protons and possibly neutrons (the 'nucleus') and an group of electrons. The protons and neutrons are much heavier than the electrons, and as a result they behave quite a bit differently. In a solid, we tend to find the nucleus roaming around a lattice point, vibrating about it with a velocity proportional to the macroscopic temperature. At zero Kelvin ('absolute zero'), we expect all such motion to cease though it's worth noting that absolute zero is more conceptual than real for a number of thermodynamic reasons. Owing to the large mass and localized behavior of the particles in the nucleus, nuclear motion tends to be surprisingly well described by classical Newtonian mechanics (think of a ball), assuming a reasonably accurate model for the interatomic interactions can be obtained. Accurate interatomic interaction models are quite difficult to produce, and is a very active area of research in physics, chemistry, and materials science.

You may have encountered the Bohr model of the atom, in which the electrons form circular orbits around the nucleus, like a planet and its moons obeying classical mechanics. A much better model, as it ends up, shows that the electrons exist in a 'cloud' that can be described by a probability distribution function obtained from quantum mechanics. This is part of the Copenhagen Interpretation of quantum mechanics, and has a number of interesting ramifications. One of the more famous is the Heisenberg Uncertainty Principle, which states that you cannot know both the position and momentum of a quantum particle, like an electron, to infinite precision. Because of their incredibly low mass, electrons are able to move at speeds approaching the speed of light in a vacuum. They also tend not to be as affected by temperatures as the nucleus until you start getting to some serious extremes (e.g. high enough to ionize the atom).

The electrons are sometimes broken into two roughly defined groups based on their role in bonding: 'core' and 'shell' electrons. The core electrons tend to be tightly bound to the nucleus while the shell electrons tend to roam a bit more freely and are more active in interatomic bonding. In metals, one model assumes that these shell electrons actually become completely unbound from the nucleus, roaming very freely throughout the metal. This mess of roaming electrons is sometimes called the 'electron sea', and is one explanation for the typically high electrical conductivity in metals.